Probabilistic Risk Analysis in Transport Project Economic Evaluation
Where presented / published:
MET research report, University of Canterbury, Nov 2011
Transport infrastructure investment decision making is typically based on a range of inputs such as social, environmental and economic factors. The benefit cost ratio (BCR), a measure of economic efficiency (“value for money”) determined through cost benefit analysis (CBA), is dependent on accurate estimates of the various option costs and net social benefits such as reductions in travel time, accidents, and vehicle operating costs. However, most evaluations are deterministic procedures using point estimates for the inputs and producing point estimates for the outputs. Transport planners have primarily focused on the cost risks and treat risk through sensitivity testing. Probabilistic risk analysis techniques are available which could provide more information about the statistical confidence of the economic evaluation outputs.
As part of his Masters in Engineering Transportation (MET), John Lieswyn undertook a research project that investigated how risk and uncertainty are dealt with in the literature and guidelines. The treatment of uncertainty in the Nelson Arterial Traffic Study (ATS) was reviewed and an opportunity to apply risk analysis to develop probabilities of sea level rise impacting on the coastal road options was identified. A simplified transport model and economic evaluation case study based on the ATS was developed in Excel to enable the application of @RISK Monte Carlo simulation software. The simplifications mean that the results are not comparable with the ATS.
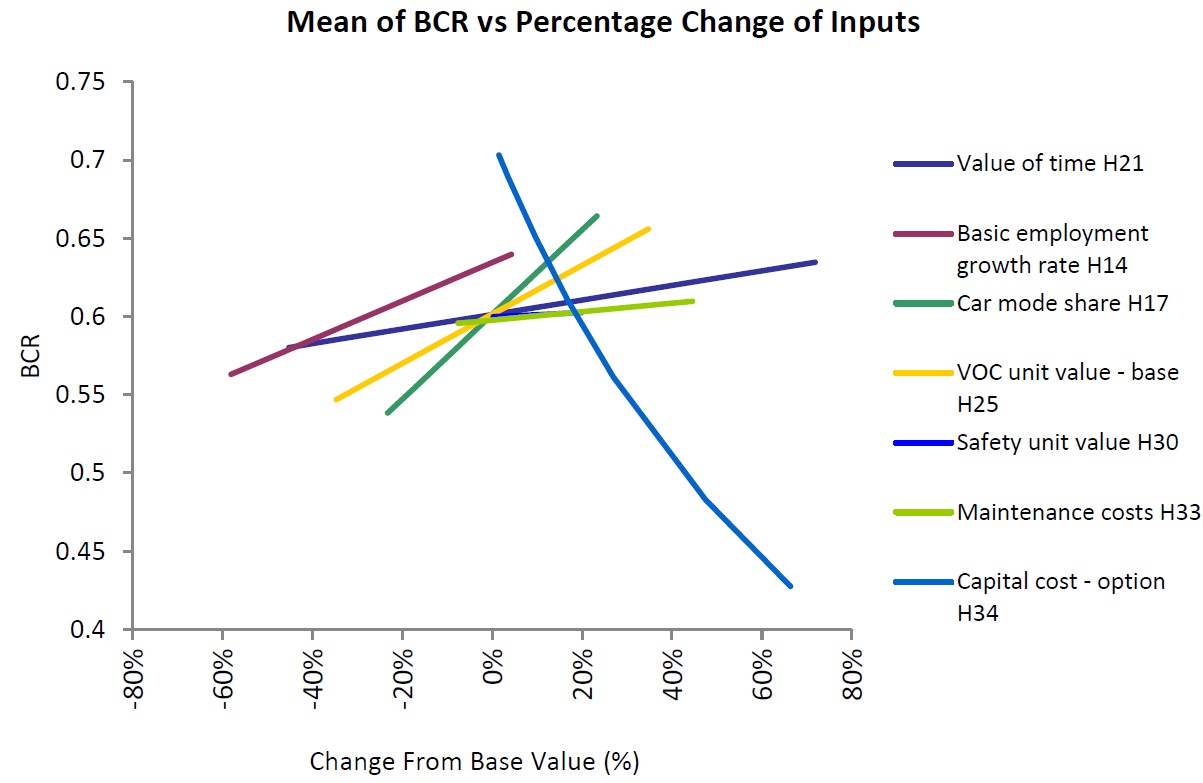
Seven input variables and their likely distributions were defined for simulation based on the literature review. The simulation of seven variables, five worksheets, and 10,000 iterations takes about 30 seconds of computation time. The input variables in rank order of influence on the BCR were capital cost, car mode share, unit vehicle operating cost, basic employment forecast growth rate, and unit value of time cost. The deterministically derived BCR of 0.75 is associated with a 50% chance that the BCR will be less than 0.6, although this probability is partly based on some statistical parameters without an empirical basis. In practice, probability distribution fitting to appropriate datasets should be undertaken to better support probabilistic risk analysis conclusions. Probabilities for different confidence levels can be reported to suit the risk tolerance of the decision makers.
It was determined that the risk analysis approach is feasible and can produce useful outputs, given a clear understanding of the data inputs and their associated distributions.
The final MET research report is available here.